What is Crystal Structure?
A crystal structure is made of atoms. A crystal lattice is made of points. A crystal system is a set of axes. In other words, the structure is an ordered array of atoms, ions or molecules.
Crystal Structure is obtained by attaching atoms, groups of atoms or molecules. This structure occurs from the intrinsic nature of the constituent particles to produce symmetric patterns. A small group of a repeating pattern of the atomic structure is known as the unit cell of the structure. A unit cell is the building block of the crystal structure and it also explains in detail the entire crystal structure and symmetry with the atom positions along with its principal axes. The length, edges of principal axes and the angle between the unit cells are called lattice constants or lattice parameters.
Table of Contents
- Recommended Videos
- Unit Cell
- Crystal Systems
- The Seven Crystal Systems
- Frequently Asked Questions – FAQs”
Unit Cell
Crystals use x-rays, which excite signals from the atom. The signals given by these atoms have different strengths, and they usually depend upon the electron density distribution in closed shells. The signals released by the atoms varies. Lighter the atoms, weaker is their signals. The mutual arrangement of atoms is also known as crystal structures. Crystal structures are derived from the physical density and chemical formulas of solids.
Unit cell can be defined as the smallest part of a component of the crystal. A group of atoms, ions or molecules, which are arranged together in a pure manner to build the crystal. The unit cells are structured in three-dimensional space, which describes the bulk arrangement of atoms of the crystal.
Crystal Systems
A Crystal System refers to one of the many classes of crystals, space groups, and lattices. In crystallography terms, lattice system and crystal, the system are associated with each other with a slight difference. Based on their point groups crystals and space groups are divided into seven crystal systems.
The Seven Crystal Systems is an approach for classification depending upon their lattice and atomic structure. The atomic lattice is a series of atoms that are organized in a symmetrical pattern. With the help of the lattice, it is possible to determine the appearance and physical properties of the stone. It is possible to identify which crystal system they belong to. In a Cubic System crystals are said to represent the element earth. They are Seven Crystal Systems and are stated below with illustrated examples.
The Seven Crystal Systems
1.Triclinic System:
It is the most unsymmetrical crystal system. All three axes are inclined towards each other, and they are of the same length. Based on the three inclined angles the various forms of crystals are in the paired faces. Some standard Triclinic Systems include Labradorite, Amazonite, Kyanite, Rhodonite, Aventurine Feldspar, and Turquoise.
2.Monoclinic System:
It comprises three axes where two are at right angles to each other, and the third axis is inclined. All three axes are of different length. Based on the inner structure the monoclinic system includes Basal pinacoids and prisms with inclined end faces. Some examples include Diopside, Petalite, Kunzite, Gypsum, Hiddenite, Howlite, Vivianite and more.
3.Orthorhombic System:
It comprises three axes and is at right angles to each other. There are different lengths. Based on their Rhombic structure the orthorhombic system includes various crystal shapes namely pyramids, double pyramids, rhombic pyramids, and pinacoids. Some common orthorhombic crystals include Topaz, Tanzanite, Iolite, Zoisite, Danburite and more.
4.Trigonal System:
Angles and axis in a trigonal system are similar to Hexagonal Systems. At the base of a hexagonal system (ross-section of a prism), there will be six sides. In the trigonal system (base cross-section) there will be three sides. Crystal shapes in a trigonal system include three-sided pyramids, Scalenohedral and Rhombohedra. Some typical examples include Ruby, Quartz, Calcite, Agate, Jasper, Tiger’s Eyes and more.
5.Hexagonal System:
It comprises four axes. The three a1, a2 and a3 axes are all contained within a single plane (called the basal plane) and are at 120°. They intersect each other at an angle of sixty degrees. The fourth axis intersects other axes at right angles. Crystal shapes of hexagonal systems include Double Pyramids, Double-Sided Pyramids, and Four-Sided Pyramids. Example: Beryl, Cancrinite, Apatite, Sugilite, etc.
6.Tetragonal Systems:
It consists of three axes. The main axis varies in length; it can either be short or long. The two-axis lie in the same plane and are of the same length. Based on the rectangular inner structure the shapes of crystal in tetragonal include double and eight-sided pyramids, four-sided prism, trapezohedrons, and pyrite.
7.Cubic System:
Cubic system is the most symmetrical one out of the seven crystal system. All three angles intersect at right angles and are of equal length. Crystal shapes of a cubic system based on inner structure (square) include octahedron, cube, and Hexaciscoherdron. Example: Silver, Garnet, Gold, and Diamond.
We have studied electromagnetic waves and the properties of x-rays in our previous sessions. Let us know what happens when the X-ray is incident onto a crystal surface by learning Bragg’s Law. This law helps understand coherent and incoherent scattering from a crystal lattice. Let us know about Bragg’s law, Bragg equation, Bragg’s derivation and its applications.
Table of Contents:
|
What is Bragg’s Law?
Bragg’s law is a special case of Laue diffraction, which determines the angles of coherent and incoherent scattering from a crystal lattice. When X-rays are incident on a particular atom, they make an electronic cloud move like an electromagnetic wave. The movement of these charges radiates waves again with similar frequency, slightly blurred due to different effects, and this phenomenon is known as Rayleigh scattering. Basically, this law explains the relationship between an x-ray light shooting and its reflection from a crystal surface.
Brag’s Law states the following:
When the X-ray is incident onto a crystal surface, its angle of incidence, θ, will reflect with the same angle of scattering, θ. And, when the path difference, d is equal to a whole number, n, of wavelength, λ, constructive interference will occur.
The exact process takes place upon scattering neutron waves via nuclei or a coherent spin interaction with an isolated electron. These wavefields that are re-emitted interfere with each other destructively or constructively, creating a diffraction pattern on a film or detector. The diffraction analysis is the resulting wave interference, and this analysis is known as Bragg diffraction.
Bragg Equation
According to Bragg Equation:
nλ = 2d sinΘ
Therefore, according to the equation of Bragg’s Law:
- The equation explains why the faces of crystals reflect X-ray beams at particular angles of incidence (Θ, λ).
- The variable d indicates the distance between the atomic layers, and the variable The variable d indicates the distance between the atomic layers, and the variable λ specifies the wavelength of the incident X-ray beam and n as an integer.
This observation illustrates the X-ray wave interface, called X-ray diffraction (XRD) and proof of the atomic structure of crystals.
Bragg was also awarded the Nobel Prize in Physics for identifying crystal structures starting with NaCl, ZnS, and diamond. In addition, to understand the structure of every state of matter by any beam, e.g., ions, protons, electrons, neutrons, with a wavelength similar to the length between the molecular structures, diffraction was developed.
Derivation of Bragg’s Law
Consider the following figure of beams in which the phases of the beams coincide when the incident angle is equal to the reflecting angle. The incident beams are parallel to each other until they reach point z. When they are at point z, they strike the surface and travel upwards. At point B, the second beam scatters. AB + BC is the distance travelled by the second beam. The extra distance is known as the integral multiple of the wavelength.
nλ = AB + BC
We also know that AB = BC
nλ = 2AB (equation 1)
d is the hypotenuse of the right triangle Abz. Ab is the opposite of the angle θ.
AB = d sinθ (equation 2)
Substituting equation 2 in equation 1
nλ = 2d sinθ
The above equation is Bragg’s law expression.
Applications of Bragg’s Law
There are numerous applications of Bragg’s law in the field of science. Some common applications are given in the points below.
- In the case of XRF (X-ray fluorescence spectroscopy) or WDS (Wavelength Dispersive Spectrometry), crystals of known d-spacings are used for analyzing crystals in the spectrometer.
- In XRD (X-ray diffraction) the inter-planar spacing or d-spacing of a crystal is used for characterization and identification purposes.
Bragg’s Diffraction
Bragg’s diffraction was first proposed by William Henry Bragg and William Lawrence Bragg, in 1913. Bragg’s diffraction occurs when a subatomic particle or electromagnetic radiation waves have wavelengths that are comparable to atomic spacing in a crystal lattice.
Solved Examples
Example 1:
The wavelength of the X-rays is 0.071 nm which is diffracted by a plane of salt with 0.28 nm as the lattice constant. Determine the glancing angle for the second-order diffraction. Assume the value of the salt plane to be 110, and the given salt is rock salt.
Solution:
Given:
Wavelength of the X-rays = 0.071 nm
Lattice constant = 0.28 nm
Plane = 110
Order of diffraction = 2
Glancing angle =?
Using Bragg’s law:
2d sin Ө = nλ
Rock salt has FCC, therefore,
Substituting the values,
Substituting in the Bragg’s equation,
Ө = 21°
Bragg’s law Conclusion
The concluding ideas from Bragg’s law are:
- The diffraction has three parameters i.e, the wavelength of X rays,λ
- The crystal orientation defined by the angle θ
- The spacing of the crystal planes, d.
The diffraction can be considered to occur for a given wavelength and set of planes. For instance, changing the orientation continuously, i.e., changing θ until Bragg’s Law is satisfied.
Technique for X-ray Diffraction
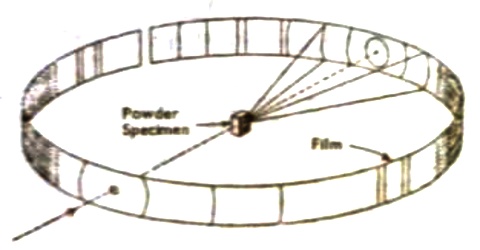
The Powder Method technique for X-ray diffraction
P. Debye and P. Scherrer devised a very simple technique for obtaining X-ray diffraction data. Their technique, known as the powder method, depends on the use of a powder of the crystalline sample instead of a single crystal. The powder is usually placed in a fine capillary or made into a rod. The experimental arrangement is shown in Figure.
Figure: experimental Arrangement for X-rat powder photograph
The little crystals constituting the powder will be oriented in all directions. There will be some oriented at the proper angle for X-ray reflection from each set of planes The diffraction pattern will be just like the one which would be obtained by mounting a single crystal and turning it through all possible angles. Since the orientations of the little crystals are random there will be reflections from a large number of planes and consequently the X-ray patient will show scattering at a large number of angles. On a flat plate film the observed pattern consists of a series of concentric circles. Bragg’s law may he applied to these lines to obtain the plane spacing. In order to derive the dimensions of the unit cell from the inter-planar spacing we must know the crystal system to which the specimen belongs. This can sometimes be determined from microscopic examination.
The X-ray powder photograph is a characteristic property of a crystal. The method may, therefore, be used for identification of the components of a solid mixture. X-ray powder diffraction is most widely used for the identification of unknown crystalline materials (e.g. minerals, inorganic compounds). Determination of unknown solids is critical to studies in geology, environmental science, material science, engineering and biology.
The Laue method is mainly used to determine the orientation of large single crystals. White radiation is reflected from, or transmitted through, a fixed crystal.
The diffracted beams form arrays of spots, that lie on curves on the film. The Bragg angle is fixed for every set of planes in the crystal. Each set of planes picks out and diffracts the particular wavelength from the white radiation that satisfies the Bragg law for the values of d and q involved. Each curve therefore corresponds to a different wavelength. The spots lying on any one curve are reflections from planes belonging to one zone. Laue reflections from planes of the same zone all lie on the surface of an imaginary cone whose axis is the zone axis.
Experimental
There are two practical variants of the Laue method, the back-reflection and the transmission Laue method. You can study these below:
Back-reflection Laue
In the back-reflection method, the film is placed between the x-ray source and the crystal. The beams which are diffracted in a backward direction are recorded.
One side of the cone of Laue reflections is defined by the transmitted beam. The film intersects the cone, with the diffraction spots generally lying on an hyperbola.
Transmission Laue
In the transmission Laue method, the film is placed behind the crystal to record beams which are transmitted through the crystal.
One side of the cone of Laue reflections is defined by the transmitted beam. The film intersects the cone, with the diffraction spots generally lying on an ellipse.
Crystal orientation is determined from the position of the spots. Each spot can be indexed, i.e. attributed to a particular plane, using special charts. The Greninger chart is used for back-reflection patterns and the Leonhardt chart for transmission patterns.
The Laue technique can also be used to assess crystal perfection from the size and shape of the spots. If the crystal has been bent or twisted in anyway, the spots become distorted and smeared out.













